How the Chroma Tunes Itself
By David Clarke [21030085++] <ac151@ncf.ca>Unlike older analog keyboards that required manual adjustment and tuning of the voices via multiple potentiometers per voice, all tuning in the Chroma is done under the direction of the computer.
We're all familiar with the flashing LEDs as the Chroma starts up. This is not just a meaningless light show - each flash actually represents one of the 16 channels being tuned.
The Chroma tunes both the oscillators and the filters in a channel. The auto-tune doesn't have 'ears' like we do. We take it for granted that somehow the tuning gets done - but have you ever wondered exactly what it is doing?
Contents
- Oscillators – Scaling and Offset
- Filters – Scaling and Offset
- Tuning Quirks – Oscillator Linearity and Auto-Tune Repeatability
Oscillators
Like most older synthesizers, the frequency of the oscillator is adjusted by a 'control voltage.' In the case of the Chroma, this voltage is under control of the embedded processor.
While the oscillators are nominally set up to change frequency by one octave for each half volt of control voltage change, natural variation in component values will mean though that each oscillator will be slightly different, and won't have an exact half-volt/octave response.
Even if the scaling was exact - natural variation may mean the same voltage may not result in exactly the same note on different voice boards.
Tuning of the oscillators is a two-phase process. First, the system needs to ensure that all channels have exactly the same scaling (so that the computer can treat them all the same way). Second, the system needs to be configured so that the same voltage will result in the same note on each voice board (e.g., that the voltage for an 'A' on one channel would also be an 'A' on another channel).
Oscillator Scaling
The Chroma knows that it wants to have all the oscillators have the same scaling - but it doesn't know in advance what scaling exists.
Ideally the scaling will have a relationship like is shown in the figure below:

In reality each channel may have different responses, perhaps as shown below:

The CPU wants to be able to adjust the control of the oscillators so that it will have a consistent method to achieve output frequencies independent of the variations in oscillator hardware. To do this, the CPU wants to be able to 'level out' the behaviour of the oscillators, and have them all behave the same.
The graphs show a voltage response. In reality, a CPU itself doesn't output an analog voltage - it is a digital computer. In order to produce a voltage, the CPU sends a digital value to a digital to analog converter (DAC), and the output of the DAC is what goes to the oscillator.
The maximum voltage produced by the DAC is based on an input Reference Voltage. If the reference voltage is 5v, then the maximum output is 5v. If the reference voltage is 3v, then the maximum output is 3v.
If we can control the voltages that the DAC will output, and can do this on a oscillator-by- oscillator basis, then we can match the behaviour of the oscillators.
Inside the Chroma there are two DACs. There is the main DAC, which is responsible for controlling the main output, and there is a 'reference DAC', a unit which allows the CPU to also control the reference voltage which is fed to the main DAC. It is this reference DAC that can be used to even out the response of the electronics.
To actually perform the tuning, the Chroma requests two notes to be produced. These notes are nominally 6 octaves apart.
6 octaves equates to doubling the frequency 6 times (e.g., 2x2x2x2x2x2 = 64.)
Stated another way - notes 6 octaves apart will differ in frequency by 64 times.
Looking at this again in a different way, the time needed for one period of a low note should be the same amount of time as 64 periods of a note 6 octaves higher.
The Chroma's CPU tries to use this relationship. Specifically - the Chroma sets the reference DAC to a mid-scale value and then sets the main system DAC to a particular value for a high frequency note. It measures the time for 64 periods of that high frequency.
The system then sets the main DAC for a note 6 octaves lower. It then measures the time for 1 period of that choice.
Based on the discussion above, the two time measurements should be the same. Any difference between the two is representative of a system that is not properly scaled.
Due to natural variability, the two measurements will not normally be exactly the same and some adjustment is required.
Finding a reference DAC value so that "64x high period" = "1x low period" could be done by simply stepping through all the possible reference DAC values and determine which one which produces the closest match between the two timing measurements. This would certainly be functional - but it would not be quick.
The reference DAC is 8-bits wide, and so there are 256 possible values. The low frequency used to tune is approximately 144Hz. The nominal period then would be about 7mS. (The high frequency is approximately 9200 Hz).
Both the low frequency and high frequency are measured during one attempt, so that would take 14mS to complete. If each of the 256 possible values were tried, that would equate to 256 x 14ms, or just over 3 seconds and this would be the time just to tune a portion of the oscillator on one channel. This is way too long in a real-world scenario, especially when considering that this adjustment needs to be made for each of the 16 channels.
Obviously, a faster approach is required.
As it happens, instead of trying all 256 possible reference DAC values - a calculation can be done to determine the same value.
In terms of theory, the slope of the lines in the earlier figures need to be adjusted to adjust the span of the octave range. The slopes depend on the value of the reference DAC.
Ideally, the relationship between voltage input and octave (frequency) output is linear. Knowing that the reference DAC controls the slope of the line the mathematical question becomes:
Given the slope of a line for a given reference DAC value (measured), what reference DAC value would be needed to achieve a desired slope.
Looking at the plots and expressing them mathematically we have:
![]()
Voltage is directly related to the main DAC (Mdac) values, so we actually have a relationship like the following:
![]()
For the Chroma implementation, the two test points differ by 6 octaves, and those test point frequencies are achieved by two different values written to the Main DAC. Expressing that mathematically we have:
![]()
In the actual system, we can determine the 'measured' slope, as below:
![]()
The Chroma can't directly measure frequency (hence can not measure octaves), but it can measure time. Since it can measure time, it can determine the period of waveforms.
Time and octave ranges relate to one another logarithmically. Thus, knowing we can measure a period (time) for a given main DAC value, the following can be determined:
![]()
where the Mdac values represent the different values written to the main system DAC. t2 and t1 represent the time periods for measurement 2 and 1, respectively.
We want to adjust our measured slope to equal our desired/needed slope. Mathematically that means we want:
![]()
where N represents a proportionality factor.
While the reference DAC (Rdac) does control the slope achievable by the main DAC, we haven't yet determined what the relationship is between the Rdac value and the slope.
Looking at the Chroma schematic we have:

Z20 is the reference DAC, and the "REF" indication at the middle right of the excerpt is the reference voltage input into the main DAC.
We can control the output of Z20 (reference DAC), but we need to determine how those changes affect the voltage applied to the reference input on the main DAC.
Working backwards, we can see that Z21B (and the resistors surrounding it) form a basic differential amplifier. The general differential amplifier has the following form:

Through conventional circuit analysis, the output of this circuit is described by:
![]()
Relating the general circuit reference designators to those in the Chroma implementation we have:
- Vout = Vref (Mdac)
- V1 = Output of Rdac = -Vinrdac * (Rdac val / 256)
- R2 = R41
- R1 = R40
- R3 = R68 + R42
- R4 = R43
- V2 = Vanalog (i.e., 5V analog power rail)
Substituting these values into the equation above we have:
The voltage available at the input to the reference DAC is essentially Vanalog (the main analog voltage supply); however, there will be some voltage drop due to R68. Taking this slight drop into account we have:
![]()
Substituting this into the main equation we now have:
Simplifying the expression gives us:
![]()
This expression gives us the relationship between the reference DAC value and the reference voltage provided to the main DAC.
As noted earlier, the voltage provided to the main DAC relates to the output 'slope'.
For the tuning procedure in the Chroma, the initial set of tuning measurements are done with a centre-scale reference DAC value. Specifically, for the measurements, the Rdac_val is set to 128.
The system slope measurements (mentioned above) are calculated for two different MDAC measurements when Rdac_val = 128. What we really want to know is, what Rdac_val is needed such that we adjust the slope to have the correct value. In terms of equations, we want to solve for:
![]()
Substituting the available expressions into this equation we have:
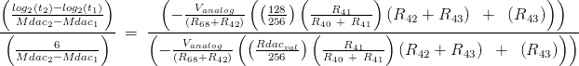
We then want to solve this for Rdac_val.
Simplifying we have:

Solving for Rdac_val we get:

Now, in the case of the Chroma - we don't actually measure both times on the same scale; rather, we measure one with a 1x reference, and the other with a 64x reference. That means, what we're really measuring is log (t*64), so, log(t2) is actually (log t*64) = log t + log 64. That changes the equation to:

What this equation tells us is that as long as we know the values of the resistors used, can measure the two times in question (and can calculate their logarithms), we can mathematically calculate the needed reference DAC to set the desired scaling of the oscillator.
Processors are quick at performing calculations - thus using this method is much faster than attempting to use a brute force method of trying all reference DAC values.
We can now look at the real values at hand. For the implementation from the service manual we have:
- R40 = 105K (1%)
- R41 = 7.5K (1%)
- R42 = 15K (1%)
- R43 = 13K (1%)
Placing these in the equation we have:

![]()
![]()
![]()
The small CPU in the Chroma can only do integer math, so expressing the equation in terms of full integers we have:
![]()

or:
![]()
This is the exact equation used in the Rev 14 Chroma firmware, where D is:
![]()
So - we've determined that the desired scaling can be achieved by manipulation of a reference DAC value - and then derived an equation to determine the needed reference DAC value based only on two time measurements. This calculation was then found to be what was implemented in the Chroma's firmware.
Since only two measurements are needed, tuning is quick only taking about 14mS total for this portion of the tuning work.
Oscillator Offset
The second part of the oscillator tuning process involves calculating the correct value for the main DAC, based on the key pressed (e.g., frequency requested). That is to say, even once the volts/octave scaling is correct, the system still needs to know how to specifically output a desired note.
The idea is that each channel may need to have an 'offset' added or subtracted to ensure that when a value is presented to the main DAC that the desired note/frequency is produced.
The difference between the period commanded and the period expected represents the 'offset' needed for that voice to sound at the desired note.
For instance, if the computer would like to output a frequency of 440 Hz, but the system electronics naturally produces 442 Hz, then the computer should know (in advance) to adjust the value being requested by "2 Hz" to ensure that the actual desired value is produced.
This offset value (2 Hz in this example) is stored in the channel definition and is added to each transaction to scale the system to match the notes.
In terms of mechanics, firmware writes a fixed value (a high frequency value) to the main DAC. It then measures the period associated with that value written. The period is made linear to notes by taking its logarithm.
Specifically the code calculates:
y = (LOG(time) / LOG(2)) - 7) * 8192
where 'time' is the period measured, and to be valid should be between 0x0100 and 0x7FFF.
The output of the calculation (y) will range from 0x2000 to 0xFFFF.
The desired/nominal result for an MDAC value of 0x2c0 is 53821, so after the calculation above, 0xd23d (53821) is subtracted. The difference represents an offset of what was asked for to what was received.
No further calculation is required. The resulting value is stored for that oscillator, and will automatically be used in all oscillator manipulations, to ensure intended scaling.
Notes: The main DAC is only 12-bits wide, so the offset attempts to be nominally around 0x400 - or half of 12 bits.
The other affect of the main DAC size is that the smallest adjustment (1 bit) is set up in such a way that the lowest control for the DAC is in terms of a 32nd of a semi-tone. That means, a 1-bit error of the offset will result in an error/misalignment of the root note by a 32nd of a semitone (e.g., approximately 3 cents)
Filters
If the Chroma only had one filter, and it was only controlled by a front-panel slider, then it may be sufficient to simply know that moving the slider would open or close the filter - and the exact amounts may not matter too much.
Since the Chroma has 16 filters, a simple slider approach will is not viable.
Similar to the case for the oscillator scaling, we want to have a method to ensure that all the filters are controlled and react in a similar way.
For this reason, the filters need to be tuned - both for response (scaling) as well as frequency (offset).
For the filter tuning, the oscillators are muted. The filter is set to Low Pass, and the resonance is set to maximum, which is the value to make it self-resonate.
While filters and oscillators are not normally considered to be similar - when the filter is resonating - it is effectively behaving like an oscillator. Because of that, it can now be 'tuned' like was previously done for the oscillators.
Filter Scaling
The filter used is the CEM3550. The nominal scaling of the CEM3350 is 19.6mv/Oct.
The input to the filter is through a voltage divider using a 38.3k and 1.87k resistor, generally resulting in a reduction of the raw control voltage from the DAC by a factor of 21.
With the scaling, the control voltage generated by the DAC is again similar to the oscillators, resulting in just under 0.5v/octave scaling.
(Note: Over different voice card revisions, the value of the '38.3k' resistor noted above has changed, resulting in a slightly different centre range for the filter. Refer to FCN2-001.)
For filter scaling (just as was the case for oscillator scaling), two test voltages are used and then measurements are made. The identical steps as with the oscillators are taken for the filter - except that the filter measurements are made over 3 octaves instead of 6 for the oscillators.
The two measurements generate voltages that are approximately 1.406volts apart.
Filter Offset
The filter offset mirrors that which was done for the oscillator. With the scale correction value in place, the filter is requested to go to a known, fixed frequency (high frequency). The period of the requested frequency is measured, and any required offset correction is determined and stored on a per-channel basis.
Tuning Quirks
Oscillator Linearity
The earlier oscillator scaling calculation was based on the assumption that the oscillator had a perfectly linear 'volt/oct' relationship.
In truth the oscillator circuitry is not 100% linear, and in actual Chroma usage, the lowest and highest notes are a bit lower than desired, resulting in a 'bowed' response.
Given that the tuning algorithm assumes a linear relationship, the non-linear behaviour has the effect of not allowing to be tuning to be 100% 'in tune' across the keyboard.
For instance, using a digital tuner on the output of the Chroma will tend to show that if you adjust 'tune' so that the lower keys on the board are 'in tune', then as you traverse higher and higher up the scale, the tuning will tend to get more and more sharp, until you get a certain point, and then start to flatten out again.
The general oscillator (4151) used is specified to have a linearity of better than 0.2%. 0.2% represents about 3.46 cents of tuning difference. The internal tuning control of the Chroma is generally in terms of 1/32nd of a semitone, or just about 3 cents.
In a worse case you could be off as much as 6 or 7 cents from absolute perfect tune.
Auto-Tune Repeatability
The offset calculation performs a single time measurement to determine how to adjust for actual note output.
Any errors in that calculation will directly result in a slight shift of the entire keyboard response. It has been observed on multiple Chroma keyboards that the design is such that there is some natural variation in this measurement (e.g., due to noise sources on the board, switching, etc.) This can most easily be seen by attaching a digital tuner to the Chroma and adjusting for perfect tune, and then repeatedly retuning the channel, using the same key reference for each trial. It will be seen that the majority of tune requests will result in the same tune value - but some will be seen to 'jump' up or down a couple cents of tuning.
This appears to simply be part of the Character of the Chroma, and if seen does not represent something different in your keyboard vs. someone else.
The actual variations are very small (e.g., 1/10th of a percent). ![]()

